Sonora.ID - Simak contoh soal mean, median, modus lengkap dengan kunci jawabannya supaya bisa menjadi pembelajaran di rumah.

Dalam statistika, suatu data berkelompok biasanya menggunakan ukuran pemusatan data agar memberi gambaran yang lebih jelas, demikian seperti dikutip dari Kompas.com.

Nah, ukuran pemusatan data tersebut meliputi mean, median dan modus.

Baca Juga: 30 Contoh Soal Olimpiade Matematika SMP Lengkap dengan Jawabannya

Pengertian Mean, Median, dan Modus

Secara sederhana, mean, median, dan modus dalam statistika dan matematika yakni sebagai berikut.

• Mean adalah rata-rata suatu data.
• Median adalah nilai tengah suatu data setelah data diurutkan.
• Modus adalah nilai yang paling sering muncul dalam suatu data.

Contoh Soal Mean, Median, dan Modus

Berikut ini contoh soal mengenai mean, median, dan modus lengkap dengan kunci jawabannya dirangkum.

1. Diketahui hasil nilai matematika Kiara, Danar, dan Jeje masing-masing 8, 6, dan 10. Berapa nilai mean dari nilai matematika ketiganya?

Mean = Jumlah total data : Banyak data
Mean = Total nilai Kiara, Danar, dan Jeje : 3 Orang (Kiara, Danar, dan Jeje)
Mean = (8 + 6 + 10) : 3
Mean = 8

Jadi, mean atau rata-rata nilai Kiara, Danar, dan Jeje adalah 8.

Baca Juga: 50 Soal Ujian Sekolah Bahasa Indonesia Kelas 6 dan Jawabannya

2. Tentukan nilai mean dari data berikut ini!
7, 7, 7, 8, 8, 9, 9, 9, 9, 10

Mean = Jumah total data : Banyak data, itu artinya kita harus menghitung nilai berdasarkan jumlah frekuensi.

Cara menghitung jumlah total data adalah sebagai berikut:

• Pada nilai 7, jumlah frekuensinya 3. Cara menghitungnya adalah 7 x 3 atau 7 + 7 + 7, hasilnya adalah 21.
• Pada nilai 8, jumlah frekuensinya 2. Cara menghitungnya adalah 8 x 2 atau 8 + 8, hasilnya adalah 16.
• Pada nilai 9, jumlah frekuensinya 4. Cara menghitungnya adalah 9 x 4 atau 9 + 9 + 9 + 9, hasilnya adalah 36.
• Pada nilai 10, jumlah frekuensinya 1. Cara menghitungnya adalah 10 x 1 atau hasilnya adalah 10.

Total data = 21 + 16 + 36 + 10
               = 83

Cara menghitung banyak data adalah menjumlahkan seluruh angka frekuensi, yaitu 3 + 2 + 4 + 1 = 10.

Mean = 83 : 10
Mean = 8,3
Jadi, mean atau rata-rata dari data di atas adalah 8,3.

3. Diketahui sebuah data adalah sebagai berikut:
3, 5, 2, 7, 9, 1, 7, 5, 3, 8, 10, 12, 5
Berapa nilai median dari data di atas?

Hal pertama yang harus kita lakukan adalah mengurutkannya dari terkecil hingga terbesar, hasilnya adalah 1, 2, 3, 3, 5, 5, 5, 7, 7, 8, 9, 10, 12.

Setelah itu kita harus mengetahui jumlah data, yaitu ada sebanyak 13 data. Karena jumlah data ganjil maka kita bisa langsung menentukan median.

Caranya adalah dengan melihat nilai yang berada di tengah, yaitu nilai di urutan ketujuh. Jadi, median dari data tersebut adalah 5.

Jika ingin mengetahui cara menghitung cepat, kita tinggal menghitung dengan rumus berikut:

Median (Me) = (jumlah data + 1) : 2
Me = (13 +1) : 2
Me = 14 : 2 = 7
Nilai ke-7 dari data di atas adalah 5.

Baca Juga: Contoh Soal Kombinasi Lengkap dengan Pembahasan Jawabannya

4. Berapa modus dari data dalam tabel ini?

Nilai	6	7	8	9	10
Frekuensi	3	7	5	8	2

Bisa kita langsung dari soal pada tabel kalau nilai yang paling sering muncul adalah 9. Hal itu karena nilai 9 muncul sebanyak 10 kali.

Jadi, modus dari data di atas adalah 9.

5. Diketahui data nilai ulangan matematika, berikut: 7,5,4,6,5,7,8,6,4,4,5,9. Tentukan mean, median, dan modusnya!

Data saat diurutkan: 4, 4, 4, 5, 5, 5, 6, 6, 7, 7, 8, 9

Ada 12 data nilai, maka cara menentukannya sebagai berikut:

• Mean
  Rumus mean = Jumlah semua nilai (∑x) / banyaknya data (n)

Mean = 4+4+4+5+5+5+6+6+7+7+8+9
Mean = 70 : 12 (banyaknya data)
Mean = 5,83

Jadi, rata-rata data nilai matematika yakni 5,83.

• Median

Rumus median = 

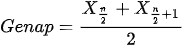
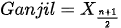
Karena banyak data yakni 12 atau genap, maka pakai rumus median genap, diperoleh:

• Modus

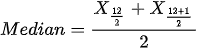
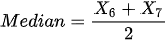
Nilai yang sering muncul yakni 4 dan 5.

Baca Juga: Rumus Cepat Rambat Gelombang dan Contoh Soal beserta Jawabannya

6. Nilai ulangan matematika Ani adalah 9, 7, 8, 9, 10, 6, 7, 9, 9. Carilah mean, median, modusnya!

Data setelah diurutkan: 6, 7, 7, 8, 9, 9, 9, 9, 10.

Banyaknya data yakni 9, maka untuk mencarinya:

• Mean

Jumlah data = 6+7+7+8+9+9+9+9+10 = 74
Mean = 

 = 8,22

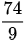
Jadi, mean atau rata-rata dari data tersebut adalah 8,22.

• Median

Median = data ke-

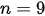
            = data ke-
            = data ke-

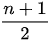
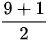
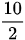
Median = data ke-5. Data ke-5 = 9

• Modus

Nilai yang paling sering dalam data yakni 9.

7. Di bawah ini terdapat data jumlah siswa kelas 7 SMP Rukun. Terdapat 4 kelas 7 di SMP Rukun, dengan jumlah siswa laki-laki dan perempuan yang tidak merata. 

Kelas/Jenis Kelamin	Kelas 7A	Kelas 7B	Kelas 7C	Kelas 7D
Perempuan	18	17	11	10
Laki-laki	12	13	19	15

Hitung rata-rata jumlah siswa laki-laki dan rata-rata jumlah siswa perempuan kelas 7 SMP Rukun!

•  Mean jumlah siswa laki-laki

Cara menghitung mean yaitu dengan menjumlahkan seluruh jumlah siswa laki-laki dan perempuan, kemudian dibagi dengan jumlah kelas yang ada. 

Mean jumlah siswa laki-laki = jumlah seluruh siswa laki-laki kelas 7 : jumlah kelas 7
Mean jumlah siswa laki-laki = (12 + 13 + 19 + 15) : 4
Mean jumlah siswa laki-laki = 59 : 4
Mean jumlah siswa laki-laki = 14,75

Jadi, mean atau rata-rata jumlah siswa laki-laki di setiap kelas 7 SMP Rukun yaitu 14 siswa. 

• Mean jumlah siswa perempuan

Mean jumlah siswa perempuan = jumlah seluruh siswa perempuan kelas 7 : jumlah kelas 7
Mean jumlah siswa perempuan = (18 + 17 + 11 + 10) : 4
Mean jumlah siswa perempuan = 56 : 4
Mean jumlah siswa perempuan = 14

Maka, mean atau rata-rata jumlah siswa perempuan di setiap kelas 7 SMP Rukun yaitu 14 siswa. 

Baca Juga: 10 Contoh Soal Silogisme dan Jawabannya, Untuk Latihan Masuk Perguruan Tinggi atau CPNS

8. Kelas 7C SMP Merdeka baru saja melaksanakan ujian matematika. Ada 15 siswa yang mendapatkan nilai di atas 70, berikut data nilanya. 
75  80  72  76  86  90  100  78  95  85  78  72  80  95  72
Berapa median dari data tersebut?

Median dari data tersebut yaitu dengan mengurutkan data dari yang terkecil ke terbesar. Kemudian, jika banyaknya data genap, maka median adalah rata-rata dua nilai di tengah. 

Namun, jika jumlah datanya ganjil, maka kita hanya perlu mencari angka yang berada di tengah. 

Pengurutan data: 72  72  72  75  76  78  78  80  80  85  86  90  95  95  100  

Median: 80.

9. Diketahui hasil ulangan IPS  siswa kelas V adalah 6, 7, 8, 8, 5, 9, 8, 7, 9, 6. Carilah rata-rata dari nilai tersebut!

Langkah pertama, kita perlu untuk mengurutkan semua angka dari nilai yang terkecil hingga terbesar, menjadi 5, 6, 6, 7, 7, 8, 8, 8, 9, 9.

Setelah itu, kita akan menghitung jumlah keseluruhan dan banyak data.

Jumlah keseluruhan data= 5 + 6 + 6 + 7 + 7 + 8 + 8 + 8 + 9 + 9 = 73

Banyak data= 10. Jadi, rata-ratanya (mean) adalah 73 : 10= 7,3.

10. Diketahui hasil ulangan matematika siswa kelas V adalah 6, 7, 8, 8, 5, 9, 8, 7, 9, 6. Carilah median dari nilai tersebut!

Pertama, tetap urutkan dari nilai terkecil terlebih dauhulu, sehingga menjadi 5, 6, 6, 7, 7, 8, 8, 8, 9, 9.

Karena jumlahnya genap, maka data paling tengah sudah pasti dua nilai, bukan satu. Coba perhatikan.

5, 6, 6, 7, 7, 8, 8, 8, 9, 9.

Nah, setelah ditemukan dua nilai paling tengah, Langkah selanjutnya adalah menghitung rata-rata kedua angka tersebut.

7 + 8 = 15 : 2 = 7,5. Jadi, median dari data tersebut adalah 7,5.

Baca Juga: Contoh Soal Pilihan Ganda Kompleks dengan Kunci Jawaban, Lengkap!

Nah, itulah tadi contoh soal mean, median, modus, dan jawabannya. Semoga bermanfaat!